付注

実質GDP等への影響推計

(1) 概要

経済政策不確実性（EPU）指数の経済・金融への定量的な影響を推計する上では、先行研究で一般的に用いられているベクトル自己回帰モデル（Vector Autoregression Model、VARモデル）を使用する。VARモデルは、ある変数を自身の過去の値によって回帰する自己回帰モデルを多変量に拡張したものであり、一定の制約を課すことで、構造的な（互いに無相関な）ショックを識別し、それによるモデル内の各変数への動学的な影響を分析することができる。

(2) 推計モデル

EPU指数、G20諸国の実質GDP、世界貿易量、米国長期金利、米国株価の5変数について、次のVARモデルを考える。

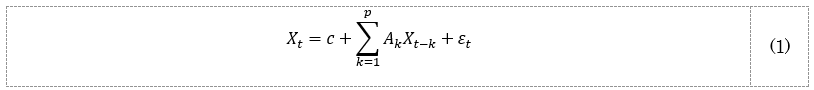
ここで、X_tは時点tの5変数が上記の順に並んだ列ベクトル、cは定数項の列ベクトル、Aは係数行列、pはVARモデルのラグ次数、ε_tはt期の撹乱項の列ベクトルである。この誘導型VARは、それぞれの変数を被説明変数、自身と他の4変数のラグ（過去の値）を説明変数とする5本の回帰式を表しており、各回帰式は最小二乗法により推計することができる。

ε_tの要素は各回帰式における予期せぬ変動を表しているが、互いに相関している可能性があることから、それぞれを構造的な「不確実性ショック」や「GDPショック」等と呼ぶことは適当でない。誘導型の撹乱項ε_tから t期における構造的なショック（u_tとする）を識別するために、先行研究にならい、「不確実性ショックは全ての変数に同一期間内に影響を与える一方、他の構造ショックがEPU指数に影響を与えるのは翌期以降になる」と想定する439。この想定の下では、ε_tの分散共分散行列のコレスキー分解によって得られる行列Pを用いて、構造ショックu_tは次のように算出することができる。

行列Pは対角成分より上が0となる下三角行列であるため、u_tの最初の成分である構造的な不確実性ショックu^unc_tは、（1）式のEPU指数の回帰式における撹乱項目ε_t^EPUを用いて、

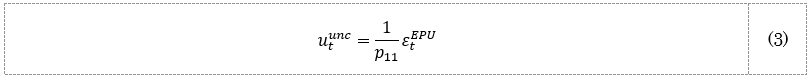
と求めることができる。ここで、p₁₁は行列Pの (1,1) 成分であり、ε_t^EPUの標準偏差となる。

こうして算出した構造的な不確実性ショックと、（1）式の係数行列Aの推計値を合わせて用いることで、不確実性ショックが発生した時の各変数への影響をインパルス応答関数として計算することができる。

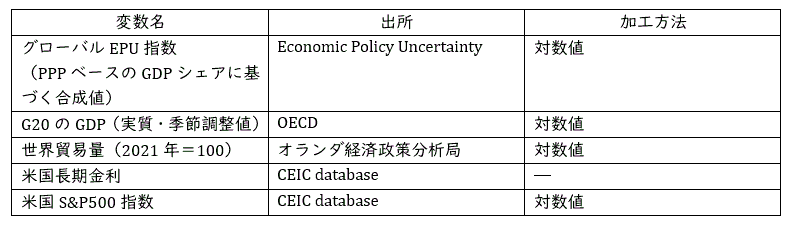
(3) データ

2000年第1四半期～2024年第4四半期のデータを用いて、各変数とも階差を取らずにレベルのまま推計を行った（t：四半期）。また、外生変数として、2020年第2四半期に1（他の期間はゼロ）の値を取る新型コロナウイルス感染症拡大ダミーを含めた。VARモデルのラグ次数は p=4とした。

(4) シミュレーション方法

本文の第I-3-2-2図では、2025年初に不確実性が急増した影響を試算した。VARモデル自体は、GDP等のデータが得られる2024年第4四半期までを推計期間としているが、各種係数が安定しているとの想定の下、（1）式の誘導型VARの係数を用いて2025年第1四半期のEPU残差を算出し、それを (3)式に代入することで2025年第1四半期440の不確実性ショックu^unc_2025Q1を計算できる。第I-3-2-2図は、そのインパルス応答関数を見たものである。